
La respuesta es bastante obvia, pero sigue leyendo y encontrarás otras cuestiones no tan obvias o conocidas alrededor de esta historia
«La respuesta corta es, por supuesto, no, puesto que surgió inicialmente sólo como un ejercicio para corregir la demostración «onto(i)lógica» del medieval Anselmo de Canterbury de que Dios existe, que le pareció tan absurda e increíblemente mala desde el punto de vista de la Lógica que intentó corregirla como profesor de dicha disciplina, como si Anselmo hubiera sido un alumno suyo, para que al menos fuera algo más correcta en lo que pudiera atañer a esta disciplina.
Sin embargo, Kurt Gödel sabía que lo que estaba haciendo era perfeccionar un procedimiento inútil en sí mismo por los resultados, puesto que incluso si hubiera podido servir lógicamente para algún fin, sin la posibilidad de contrastación con algo que realmente diera en el mundo real prueba de la existencia de lo que quiera que se desee concebir como el objeto «un dios» no serviría en lógica para nada. Su utilidad era simplemente didáctica para mostrar cómo habría debido ser el planteamiento más o menos inteligentemente coherente que habría debido hacer el de Canterbury.
Ahora verán por qué.
Desde niño, a Gödel le gustaban mucho los problemas paradójicos de lógica contraponiendo funciones semánticas y sintácticas y basados en el uso de un lenguaje y un metalenguaje juntos, a pesar de saberse que esto no se puede hacer porque se usan operadores, léxico, sintaxis, etc engañosos al efecto, ya que comparten denominaciones no distinguibles –salvo que se haga en un análisis por voluntad propia– por tratarse ambos de lenguajes, lo que contribuye al equívoco. Cosas como
un griego decía que todos los griegos son unos mentirosos, por lo tanto ¿su aseveración es verdadera o falsa?
donde lo ingenioso era ver cómo plantearlos de otro modo, difuminando lo más ampliamente la posibilidad de distinguir lenguaje de metalenguaje, cuestión a la que se prestan todo tipo de desarrollos y extensiones de la Lógica que impidan caracterizaciones simples y acepten valoraciones más o menos subjetivas en el uso cotidiano del lenguaje natural. Y no estuvo mal su interés por estas curiosas diversiones, porque precisamente a partir de estas inquietudes generó a muy temprana edad los, sin embargo, muy serios teoremas de incompletitud de la matemática que le dieron fama.
Para hacer las correcciones al incorrecto procedimiento de Anselmo de Canterbury del que partió Gödel, usó el conocimiento de todos los desarrollos que en lógica y sus extensiones se habían hecho desde la Edad Media, haciendo varias versiones sucesivas de ello que nunca publicó precisamente porque se trataba sólo de una diversión intelectual. Utilizó básicamente una extensión de la Lógica llamada lógica modal que consiste en poder hacer valoraciones que califican la tipología del modo de verdad de los juicios en cada unidad proposicional; modificadores que podrían entenderse como advervios del tipo necesariamente, siempre, ocasionalmente, posiblemente, etc y sus correspondientes negativos.
El argumento original de Anselmo de Canterbury podría resumirse en lo siguiente: «Dios, por definición, es aquello de lo cual nada mayor puede concebirse, por lo cual es imposible concebir que Dios no existe dado que de lo contrario podríamos concebir algo mayor que él, es decir, un Dios que sí exista. Y como es inconcebible que Dios no exista se entiende que existe.» Esta supuesta demostración usa argumentos de lógica modal, aunque ésta no fue formalizada hasta principios del siglo XX.
La razón por la que no se usa la lógica de predicados ya se conocía en la época de Anselmo, se puede demostrar la existencia de Dios de una forma mucho más corta (aunque menos satisfactoria): “Si no es cierto que “Dios existe implica que castigará a los buenos”, entonces Dios existe.” Esta demostración es resultado de la siguiente paradoja de la implicación lógica:
Si no es cierto que P implica Q, entonces P.
Recuerda que la implicación lógica “P implica Q” significa que si P es falso, “P implica Q” es verdadero,
y si P es verdadero, “P implica Q” es verdadero o falso según lo sea Q.
La implicación lógica presenta múltiples paradojas, como que si Q es verdadero, entonces “P implica Q” es verdadero para todo P (incluso sin que haya ninguna relación entre P y Q). Estas paradojas resultan extrañas para la intuición, rayando lo absurdo.
Para evitar estas paradojas la demostración de Gödel utiliza el sistema S5 de la lógica modal de Lewis y Langford (1932).
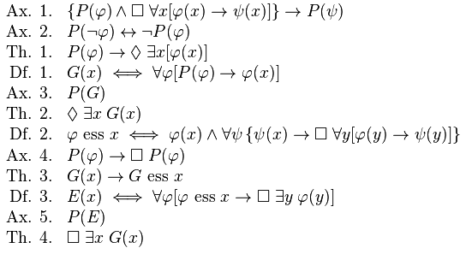
Hay varios tipos de lógica modal en función de cómo sean los axiomas de los que se parta. Un axioma es una verdad muy simple considerada incontrovertible que se entiende que puede ser verificada por todo el mundo para un ejercicio dado y de la que se parte para llegar a otras verdades por procedimientos correctos varios donde la inferencia suele ser el central. Grosso modo, podemos decir que dependiendo del conjunto de axiomas de los que partimos podemos demostrar unas cosas sí y otras no. Por ejemplo, los axiomas de los que parte la geometríca clásica sirven para describir espacios euclidianos (que suelen llamarse espacios planos) –aquí uno de los axiomas de partida es que los ángulos interiores de cualquier triángulo suman siempre 180º– pero hay otros conjuntos básicos de axiomas que permiten describir espacios esféricos (con curvatura positiva) –aquí es uno de los axiomas que los ángulos interiores de cualquier triángulo suman siempre más de 180º–, otros espacios hiperbólicos (con curvatura negativa) –aquí es un axioma que los ángulos interiores de cualquier triángulo suman siempre menos de 180º– y hasta otros espacios aparentemente imposibles para su realización física pero posibles congruentemente para el planteamiento exclusivamente lógico de dichos axiomas iniciales.
Como dije, Gödel utilizó la variante de lógica modal apellidada habitualmente como S5 en la lógica modal de Lewis y Langford, que está basada en estos tres axiomas: 1.– Si es necesario que A, entonces A; 2.– Si es necesario que A implique B, entonces si A es necesario, B también lo es; y 3.– Si es posible que A, entonces que A sea posible también es necesario. Por lo explicado ya anteriormente, esta lógica modal S5 funciona necesariamente de modo distinto a otras variantes porque en ella requiere pasos lógicos diferentes el «demostrar» algo. Sin embargo, la realidad del trabajo de Gödel sólo terminaba por demostrar que si un objeto/ente (Dios en ese caso) existe podemos afirmar que existe, 🙂 afirmación que no era ni mucho menos pretensión de Gödel sino del de Canterbury que elaboró el proceso original que estaba corrigiendo concienzuda y diversamente Gödel. Veámoslo del modo más simple en que pueda mostrarse.
Su primer axioma (Ax1) es «O bien A es P o bien no A es P» (disyunción exclusiva) –donde A y B son dos proposiciones que son semánticamente modos de ser y P una propiedad calificativa que es semánticamente «ser bueno»–. Esto es independiente de que en nuestros días comprendemos plenamente que ser bueno es algo bastante mutable y dependiente de cultura y persona, por lo que nno existe ninguna idea absoluta en sí misma de lo que es «ser bueno». Su segundo axioma (Ax2) es «Si A es P y siempre que tenemos A tenemos B, entonces B es P». De estos dos axiomas establece la primera relación lógica entre éstos, es decir, su primer teorema (T1): «Si A es P, entonces es posible que algo o alguien exista con la propiedad A».
Fijémonos que el teorema no implica que A exista, sólo que si A es una propiedad buena puede que haya algo o alguien que la tenga. O sea, por ejemplo, puede que ser altruísta sea bueno y quizá exista alguna persona altruísta, pero eso no implica que exista alguien altruísta necesariamente. Por tanto, T1 sólo «demostraría», como mucho, que quizá pudiera ser posible que existiesen personas altruístas si se dan unas determinadas condiciones. Recuérdese que en el juego de Anselmo hay que aceptarle esta primera definición porque él intenta probar que algo existe y si no define qué es ese algo, por muy estrambótico o imposible que pudiera ser a posteriori tras un análisis, no habría forma de verificar existe si lo que él dice que existe.

Tras T1 se hace una definición de un dios desde el punto de vista religioso (D1): «Un ser divino sería algo o alguien que tuviese todas las propiedades buenas». Esto implicaría que las propiedades malas e intermedias limitarían a ese ser, es decir, estarían fuera de él, tras sus límites, por lo tanto no podría ser omnipotente ni omnipresente. Pero estos detallitos escapan a un juego de demostración de lógica modal como éste, porque ninguna consideración sobre omnipotencia u omnipresencia entra en los axiomas utilizados.
Ahora aparece el axioma tercero (Ax3) que dice que «Ser divino es algo bueno», que se sigue lógicamente de la definición anterior D1.
Y de todo lo anteriormente sentado y combinado lógicamente aparece supuestamente el teorema segundo (T2) que dice que «Es posible que algo divino exista». Volvemos a llamar la atención de que estamos en la misma situación que en T1, (derivando de «Si A es P, entonces es posible que algo o alguien exista con la propiedad A») sólo «demostraría», como mucho, que quizá pudiera ser posible que existiese algo divino si ser divino es simplemente contener todas las propiedades buenas.
El axioma cuarto (Ax4) parece redundante, pero no lo es: «Si algo es bueno, es necesariamente bueno». Esto no quiere decir que lo que es bueno es bueno, sino que lo que es bueno lo es porque es necesario que sea así siempre y no puede serlo alternativamente con su contrario.
Inmediatamente tras esta declaración impone otra definición (D2): «E es la esencia de una cosa x cuando x tiene la propiedad E y la propiedad E fuerza las propiedades de x.» Como de costumbre, de muy difícil aceptación fuera del juego axiomático de la lógica modal propuesta. Pero volviendo a dicho juego, en pocas palabras, dice que todas las propiedades de algo se derivan de su «esencia», que a su vez es la propiedad generatriz de las demás propiedades de ese algo. Redundante donde lo haya, pero axiomático en este juego para ahora definir el teorema tercero (T3), que en teoría debe seguirse de todo lo anteriormente sentado en el juego lógico: «Ser divino es la esencia de cualquier entidad divina».
Inmediatamente tras esta declaración impone otra definición (D3): «Una cosa será indispensable si algo con su esencia debe existir». No volveré a hacer los comentarios anteriores de aviso que aquí corresponderían. Establecida esta definición viene el axioma quinto (Ax5): «Ser indispensable es una buena propiedad». Que hace colofón con todo lo que a Anselmo le hacía falta para su juego, si lo hubiera hecho correcto como juego en sí. En efecto, véase lo que pretendió hacer:
Quería que quedara sentado que si algo es divino, tiene, por definición, todas las propiedades buenas (D1); pero le hacía falta definir también que ser indispensable fuera una de esas propiedades buenas (Ax5), o de otro modo el juego no funcionaría. Así podía «concluir» que un ser divino debe tener la propiedad de ser indispensable (T2) y si esto es cierto entonces «debe» existir algo con la esencia divina (D3) y, de ser así, ese algo ha de ser divino (T3). Finalmente, concluye que como es posible que algo divino puede existir (T2) y es necesario que exista (T3) puede ser posible que sea necesario que exista, ergo el ser divino existe.
Sí: ya he dicho que es evidente que no funciona como sistema para demostrar que un dios existe, Kurt Gódel lo sabía y cualquier persona inteligente se da también cuenta de inmediato. De hecho, el problema del argumento inicial, el llamado «ontológico» de Anselmo, es que es tramposo desde el propio comienzo, pues es evidente que el concepto de existencia no es una «propiedad», como, por ejemplo, ya señalaron Kant y varios otros filósofos. Pero en la Edad Media era muy normal este tipo de juegos de reglas privilegiadas que en teoría servían al efecto. Sin embargo, no se daban cuenta de que por el mismo método se podía demostrar que hasta Superman o el Espaguetti universal pastafariano existen. Cualquier cosa, de hecho. Para deshacer la trampa o malformación original lo que Gödel modifica es el concepto de existencia como propiedad por la propiedad de que sea «necesaria su existencia», lo que formalmente, y sólo formalmente, permite que pueda ser aceptado por las reglas de la lógica modal, aunque sigan siendo evidentes los mismos problemas semánticos de fondo. La asunción gratuíta que hace la formulación de Gödel de lo que dice Anselmo es que en alguna parte de la realidad existe un universo con objetos con las propiedades que define. Así de descarado, porque es irrelevante para la tarea real que quiere realizar, que es corregir lógico-modalmente a Anselmo de Canterbury.
Por ejemplo, con el mismo método:
Si x es una buena propiedad entonces es posible que algo o alguien exista con dicha propiedad. Si el poder volar mediante una capa como un pájaro es una buena propiedad entonces es posible que exista algo o alguien que vuele mediante una capa como un pájaro –por muy extraño que le parezca a una persona lógica–. Ahora toca decir que algo tiene la propiedad de ser volador como un pájaro mediante una capa cuando posee toda propiedad buena, después afirmar que ser volador como un pájaro mediante capa es bueno y que, por tanto, es posible que exista algo volador como un pájaro mediante capa. Ya casi acabamos, sólo nos queda definir la multivalente propiedad «esencia» del sistema S cuando S tiene la propiedad «esencia» y esta propiedad implica «cualquier otra propiedad de S», así como afirmar que «si x es bueno entonces es necesariamente bueno» (o sea, en todos los casos posibles y sin que pueda caber lo contrario, o no sería bueno), de lo que se deriva que «si un sistema es volador como un pájaro mediante capa entonces serlo es su esencia». Ahora rematamos «recordando» que «un sistema es indispensable cuando algo con su esencia tiene que existir por fuerza», dejando claro que ser indispensable es bueno, por lo cual, «algo volador como un pájaro mediante capa tiene que existir a la fuerza». Yyyyy… ¡¡¡acabamos de demostrar la existencia de Superman!!! 🙂
Y así con cualquier otra cosa. Literalmente.
En pocas palabras, lo que se hace no es realmente demostrar la existencia de un dios llamado Dios, sino definir una supuesta característica única, exclusiva y no probada que llaman esencia, que es necesario que ese objeto o ente tenga y de la que se puedan derivar todas sus demás propiedades esenciales.
Así pues, no. Ni Gödel demostró con Lógica-Matemática que Dios existe ni tuvo jamás la pretensión de hacerlo.» [Agustín Barahona]
Tienes que Iniciar Sesión